公务员考试行测数量关系：数字推理之解题思维

1、横向递推

横向递推的思维模式是指在一组数列中，由数字的前几项，经过一定的线性组合，得到下一项的思维模式。

【示例】1/9，1，7，35，（）
A、120 　B、105 C、125 D、200

【解析】B。此题目的突破口是局部比较明显的倍数关系，1/9的9倍是下一项1；1的7倍是下一项7；7的5倍是下一项35；按照此规律括号内的数应为35的3倍，即105。

2、纵向延伸

相较于横向递推思维模式，稍为复杂的就是纵向延伸的思维模式。他不再是简单的考虑数列本身，而是把数列当中的每一个数，都表示为另外一种形式，从中找到新的规律。我们只需要把刚才的例子换一个数字，那么思维模式就完全不同了。

【示例】1/9，1，7，36，（）
A、120 　B、105 C、125 D、200

【解析】C。注意这样一个数列，如果我们把35换成36的话，我们会发现，前后项之间就没有完整的倍数变化了。明显横向递推受阻进行不下去，那么我们可以换一个方向想，用纵向延伸的思维模式，把数列中每一个数字都用另外一种形式来表述。即：9^-1、8^0、7^1、6^2，那么接下来括号应为5^3，即125。

3、构造网络

构造网络这个思维模式是近两年数字推理的一个出题趋势，广东中公教育结合近两年考过的真题为大家详解。

【示例】1，2，6，16，44，120，（）
A.164 B、176 C、240 D、328

【解析】D。从所给出的数字入手单调递增，相邻两项间的幅度变化在3倍以内，可能为等差、倍数、和数列。先看倍数关系，但相邻两项间的倍数关系没有规律，作差也没有规律，考虑两两做和3，8，22，60，164。

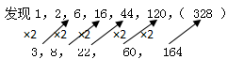
作出的和找不到明显规律，这个时候我们就带着新数列和原数列建立起网络，看一看他们有没有什么联系，我们发现“和”和原数列的下一项有完整的2倍关系。也是常用的构造网络思维模式，与原数列一起找规律。